This paper describes research done in the experimental evaluation and the development of a simplified procedure to estimate the out-of-plane behavior and strength of unreinforced masonry infill panels, and how it is influenced by existing panel damage caused by previously applied in-plane forces.
PROBLEM
Although masonry infills are not considered structural elements, they greatly affect the behavior of the structure horizontally in both the parallel (in-plane) and the transverse (out-of-plane) directions with respect to the face of the infill. Furhtermore, there was a need for a analytical model that would evaluate out-of-plane strength with the previous in-plane damage.
AIM AND SCOPE
Test and develop simplified procedure to estimate out-of-plane strength of the panels and the possible influence due to existing in-plane damage.
DESIGN AND CONSTRUCTION OF THE TEST SPECIMENS:
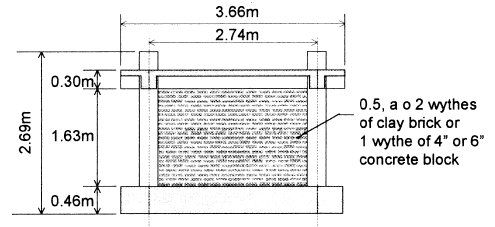
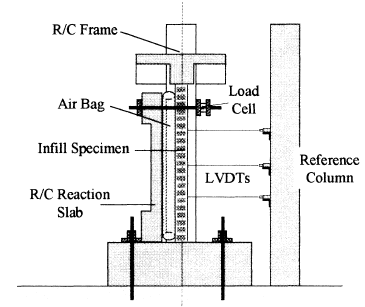
Full size test specimens consisted of a series of masonry infills placed within single-bay, single-storey,reinforced concrete frames with masonry infill. The frames were designed as strong and weak in relation to the masonry.
The tests were done using monotonic, static pressure applied via airbag.
The specimens had the following characteristics:
-------------------------------------------------------------------------------------
| Specimen | Masonry | h/t | Mortar | Compressive | In-plane | Out-of-plane |
| | type | | type | strength (MPa) | drift (%) | Pressure (kPa) |
|-----------|---------|-----|---------|----------------|-----------|----------------|
| 1 | Brick | 34 | S | 11.51 | 0.00 | 8.19 |
| 2 | Brick | 34 | N | 10.86 | 0.34 | 4.02 |
| 3 | Brick | 34 | L | 10.14 | 0.22 | 5.99 |
| 4 | Block | 18 | N | 22.90 | 0.09 | 29.78 |
| 5 | Block | 11 | N | 21.46 | 0.06 | 32.22 |
| 6 | Brick | 17 | L | 4.59 | 0.25 | 12.40 |
| 7 | Brick | 17 | N | 11.00 | 0.25 | 30.74 |
| 8 | Brick | 9 | L | 3.59 | 0.39 | 32.08 |
-------------------------------------------------------------------------------------
Where mortar type (cement:lime:sand): S (1:0.5:4.5), N (1:1:6), L (0:1:3).
CONCLUSIONS
A simplified model was developed, based on arching action:
2*fm
------ * lambda * R2 * R1
h/t
Where: lamba is a table value, R2 a boundary factor (=1 when infill is fully conected to the frame), R1 a reduction factor due to previous in-plane damages, h - infill height and t - infill thickness.
Amount of existing panel damage for R1 factor:

Values for the simplified model:
------------------------------------
| h/t | lambda | R1 (damage) |
| | | Moderate | Severe |
|-----|--------|----------|--------|
| 5 | 0.129 | 0.997 | 0.994 |
| 10 | 0.060 | 0.946 | 0.894 |
| 15 | 0.034 | 0.888 | 0.789 |
| 20 | 0.021 | 0.829 | 0.688 |
| 25 | 0.013 | 0.776 | 0.602 |
| 30 | 0.008 | 0.735 | 0.540 |
| 35 | 0.005 | 0.716 | 0.512 |
------------------------------------
The following conclusion were drawn:
- The out of plane strength of cracked infill can be appreciable. Cracked infill panels with h/t ratios as high as 34 resisted up to 6 kPa of lateral pressure;
- Panels with h/t as large as 17 can resist lateral pressures exceeding 30 kPa;
- In-plane cracking can reduce out-of-plane strength by as much as one half for slender panels;
- The developed out-of-plane strength evaluation method provides suitable lower-bound estimates;
- The designed simplified model had good correlation with the experimental data.
RECOMMENDATIONS FOR FUTURE RESEARCH
None were specified.










